Esta es una sección optativa en la que se supone que el lector está familiarizado con el cálculo integral. Si usted no ha estudiado aún integración en su curso de cálculo debe saltar esta sección o cubrirla tiempo después de haberse familiarizado con la integración.
La velocidad de una partícula que se mueve en una línea recta puede obtenerse
de conocer cuál es su posición como función del tiempo. Matemáticamente, la velocidad es igual a la derivada de la coordenada respecto del tiempo. También es posible encontrar el desplazamiento de una partícula si se conoce su velocidad como función del tiempo.
En cálculo, este procedimiento se conoce como integración, o determinación de la antiderivada. Gráficamente es equivalente a determinar el área bajo una curva.
Suponga que la gráfica de velocidad contra tiempo para una partícula que se
mueve a lo largo del eje x es como se muestra en la figura 2.11 Divídase el intervalo de tiempo tf- tI, en muchos intervalos pequeños de duración ∆tn. Según la definición de la velocidad promedio, se ve que el desplazamiento durante cualquier intervalo pequeño, como el sombreado en la figura 2.11, está dado por: Donde la suma se toma sobre todos los rectángulos de ti a tf. Ahora, a medida que cada intervalo se hace más pequeño, el número de términos en la suma aumentan y ésta se acerca a un valor igual al área bajo la gráfica velocidad-tiempo. En consecuencia, en el límite:
Advierta que en la suma se ha sustituido la velocidad promedio vn por la velocidad instantánea Como se puede ver en la figura 2.11, esta aproximación es válida en el límite de intervalos muy pequeños.
La conclusión es que si la gráfica velocidad - tiempo para el movimiento a lo largo de una línea recta se conoce, el desplazamiento durante cualquier intervalo de tiempo puede obtenerse al medir el área bajo la curva correspondiente a ese intervalo de tiempo.
En la ecuación 2.6.1 el límite de la suma se conoce como integral definida y se escribe:
Fig. 2.11 Velocidad versus tiempo para una partícula en movimiento a lo largo del eje x. El área del rectángulo sombreado es igual al desplazamiento ∆x en el intervalo de tiempo ∆tn, mientras que el área total bajo la curva es el desplazamiento total de la partícula.
Si una partícula se mueve con una velocidad constante V0, como muestra la figura 2.12 , su desplazamiento durante el intervalo de tiempo ∆t es simplemente el área del rectángulo sombreado, es decir,
∆x = v0 ∆ t (cuando v = v0 = constante)
Como otro ejemplo, considere una partícula moviéndose con una velocidad que
es proporcional a t, como se ve en la figura 2.13. Si se toma v = at, donde a es la
constante de proporcionalidad (la aceleración), se encontrará que el desplazamiento de la partícula durante el intervalo de tiempo t = 0 at = t1 es el área del triángulo sombreado en la figura 2.13:
MOVIMIENTO RECTILÍNEO.
MOVIMIENTO RECTILÍNEO.
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.
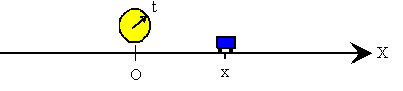
En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.
Movimiento
DESPLAZAMIENTO, VELOCIDAD Y ACELERACIÓN
La velocidad media Vx durante un intervalo de tiempo ∆t pude obtenerse determinado la distancia ∆x que recorre la partícula en ese intervalo, y observando que
La mecánica trata las relaciones entre fuerza, materia y movimiento; nos disponemos a
analizar los métodos matemáticos que describen el movimiento.
Esta parte de la mecánica recibe el nombre de cinemática.
Las siguientes son consideraciones que fundamentan dicho estudio:
· El movimiento puede definirse como un cambio continuo de posición.
· En el movimiento real de un cuerpo extenso, los distintos puntos del mismo se mueven siguiendo trayectorias diferentes, pero consideraremos en principio una descripción del movimiento en función de un punto simple (partícula).
· Tal modelo es adecuado siempre y cuando no exista rotación ni complicaciones similares, o cuando el cuerpo es suficientemente pequeño como para poder ser considerado como un punto respecto al sistema de referencia.
· El movimiento más sencillo que puede describirse es el de un punto en línea recta la cual haremos coincidir con un eje de coordenadas.
DESPLAZAMIENTO, VELOCIDAD Y ACELERACIÓN
Para comprender como se mueven los objetos cuando actúan en ellos fuerzas y momentos de rotación externos no equilibrados, es importante configurar exactas imágenes físicas y matemáticas del desplazamiento, la velocidad y la aceleración, comprender las relaciones entre estas tres cantidades.
En el proceso se imaginará un sistema que comprende tres ejes coordenados mutuamente perpendiculares y un pequeño cuerpo en movimiento, que en el curso del tiempo, describe alguna clase de trayectoria en el espacio de coordenadas.
El principio, no se tendrá interés en las fuerzas que provoca este movimiento, ni en la relación entre estas causas físicas y la trayectoria resultante.
En vez de ello, se supondrá que se conoce una ecuación de movimiento que puede resolverse para dar información explícita en todo momento acerca de la posición, la velocidad y la aceleración de la partícula.
Sólo se considerarán los aspectos geométricos del movimiento, cuyo estudio se llama cinemática.
Inicialmente se supone que, de alguna manera, la partícula objeto del estudio está limitada a moverse sólo a lo largo del eje x.
Entonces se puede describir su posición en cualquier instante t por medio de la distancia x entre el origen y la partícula, como hay un valor bien definido de x asociado a cada valor t del tiempo,
x es una función de t.
Por lo anterior será posible representar gráficamente el desplazamiento x en función del tiempo y obtener una gráfica como la de la figura (2.1)
2.2.1
Desplazamiento de un objeto que se mueve sobre el eje x graficado en función del tiempo. La cantidad ∆x/∆t representa la velocidad media en el intervalo de tiempo ∆t, mientras que el límite de esta cantidad cuando ∆t tiende a cero, que es la derivada dx/dt, representa la velocidad instantánea en el tiempo t.
De la figura 2.1 es claro que Vx es la tangente del ángulo θ, por lo que representa también la pendiente de la secante PQ que une los dos puntos de la curva que corresponde al tiempo t y al desplazamiento x + ∆x
Ahora podrá definirse la velocidad instantánea vx asociada a un instante t y el desplazamiento correspondiente x, como el límite de Vx cuando el intervalo de tiempo ∆t tiende a cero. Pero esto es precisamente la definición de la derivada de x con respecto a t; entonces,
La velocidad instantánea puede considerarse como la pendiente de la tangente en P a la curva de la figura 2.1.
Es claro que conforme ∆t y ∆x tienden a cero en el límite, la pendiente de la secante PQ se aproxima a la pendiente de la tangente a la curva en P.
Por la ecuación (2.2.2), se puede considerar que la velocidad instantánea Vx es la rapidez de variación del desplazamiento.
Fácilmente se demuestra que si la velocidad instantánea es constante, entonces la velocidad media un intervalo de tiempo es igual a la velocidad instantánea.
Si la velocidad instantánea no fuese constante, entonces la velocidad dependerá del intervalo tiempo escogido y, en general, no será igual a la velocidad instantánea al principio o al final del intervalo.
También se puede hablar de la aceleración media āx durante cierto intervalo, como el cambio en la velocidad instantánea Vx que experimenta la partícula durante aquél, dividido entre la duración del mismo,..; ∆t entonces,
OTRAS CONSIDERACIONES IMPORTANTES SOBRE DESPLAZAMIENTO, VELOCIDAD Y RAPIDEZ
El movimiento de una partícula se conoce por completo si su posición en el espacio se conoce en todo momento.
Por ejemplo, considérese un auto (que trataremos como una partícula) que se mueve a lo largo del eje x desde un punto P a un punto Q.
Su posición en el punto P es x, en el tiempo ti y su posición en el punto Q es xf en el tempo tf. (Los índices i y f se refieren a los valores inicial y final.) (Figura 2.3)
A. Un auto se mueve a la derecha a lo largo de una línea recta tomando como el eje x. Debido a que nos interesa solo el movimiento de traslación del auto se puede tratar como una partícula
B. Grafica posición-tiempo para el movimiento de la “partícula
En tiempos diferentes a ti y tf, la posición de la partícula entre estos dos puntos puede variar,.
Una gráfica con estas características recibe el nombre de gráfica de posición - tiempo, Cuando la partícula se mueve de la posición xi a la posición xf, su desplazamiento está dado por Xf - xi.
Como se sabe con la letra griega delta se indica el cambio en una cantidad.
Por consiguiente, se escribe el cambio en la posición de la partícula (el desplazamiento).
El desplazamiento no debe confundirse con la distancia recorrida puesto que en cualquier movimiento ésta es por completo diferente a cero.
VELOCIDAD PROMEDIO, INSTANTANEA Y RAPIDEZ
La velocidad promedio de una partícula se define como el cociente entre la distancia total recorrida y el tiempo total que lleva viajar esa distancia:
distancia total
Velocidad promedio = ————————
tiempo total
La unidad del SI de la rapidez promedio, igual que la velocidad, también es metros por segundo.
Sin embargo, a diferencia de la velocidad promedio, la rapidez promedio no tiene dirección, por lo tanto no lleva signo algebraico.
Conocer la velocidad promedio de una partícula no brinda ninguna información acerca de los detalles del viaje.
Por ejemplo, suponga que usted tarda 8.0 h al viajar 280 Km. en su automóvil. La rapidez promedio de su viaje es 35 Km./h. Sin embargo, es probable que usted haya viajado a diversas velocidades durante el trayecto, y la rapidez promedio de 35 Km./h resultaría de un número infinito de posibles variaciones de rapidez.
ACELERACIÒN INSTANTÀNEA
Cuando La velocidad de una partícula cambia con el tiempo, se dice que la partícula esta acelerando.
Por ejemplo: La velocidad de un automóvil aumentará cuando usted “le pise el acelerador” y disminuirá cuando aplique los frenos.
Sin embargo, es necesaria una definición más precisa de aceleración:
Supóngase que una partícula que se mueve a lo largo del eje x a una velocidad vi al tiempo ti, y una
velocidad vf tiempo tf, como se muestra en la figura 2.4a.
a) Una “partícula” que se mueve de P a Q tiene velocidad vi en t = ti y velocidad vf en t = tf.
b) Grafica velocidad-tiempo para la partícula moviéndose en una línea recta.
La pendiente de la línea recta que conecta P y Q es la aceleración promedio en el intervalo de tiempo ∆t= tf - ti.
La aceleración promedio de la partícula en el intervalo de tiempo ∆t = tf - ti
se define como el cociente ∆v/∆t, donde ∆v = vf-vi es el cambio de la velocidad en este intervalo de tiempo:
La aceleración tiene dimensiones de longitud dividida por (tiempo)2, o L/T2.
Algunas de las unidades comunes de aceleración son metros por segundo por segundo (m/s2) y pies por segundo por segundo (pies/s2).
De la misma forma que con la velocidad se pueden emplear los signos positivo y negativo para indicar la dirección de la aceleración cuando el movimiento que se analiza es unidimensional.
En algunas situaciones el valor de la aceleración promedio puede ser diferente sobre intervalos de tiempo distintos.
Por ese motivo, es útil definir la aceleración instantánea como el límite de la aceleración promedio cuando ∆t se acerca a cero.
Este concepto es similar a la definición de velocidad instantánea estudiado, la aceleración instantánea será:
Es decir, la aceleración instantánea es igual a la derivada de la velocidad respecto del tiempo, la cual por definición, es la pendiente de la gráfica velocidad-tiempo (Fig.2.4b).
Se puede interpretar la derivada de la velocidad respecto del tiempo como la tasa de cambio de la velocidad. Si a es positiva, la aceleración está en la dirección x positiva, pero, si a es negativa indica que la aceleración está en la dirección x negativa.
A partir de ahora se empleará el término aceleración con el significado de aceleración instantánea.
Puesto que v = dx/dt, la aceleración también puede escribirse:
La aceleración instantánea puede obtenerse de la grafica velocidad-tiempo.
a) En cada instante, la aceleración en la grafica a contra t.
b) Iguala la pendiente de la línea tangente a la curva de v contra t.
Es decir, en un momento unidimensional, la aceleración es igual a la segunda derivada de la coordenada x en relación con el tiempo.
La aceleración en cualquier tiempo es la pendiente de la grafica velocidad-tiempo en ese tiempo.
RELACIONES GRÁFICAS ENTRE X, V Y A
VELOCIDAD INSTANTÁNEA Y RAPIDEZ
Poder definir la velocidad de una partícula en un instante particular del tiempo, en lugar de sólo un intervalo de tiempo, la velocidad de una partícula en cualquier instante de tiempo - en otras palabras, en algún punto sobre una gráfica espacio – tiempo - recibe el nombre de velocidad instantánea. Este concepto tiene una importancia especial cuando la velocidad promedio en diferentes intervalos de tiempo no es constante.
a) Conforme el auto se mueve a lo largo del eje x, y Q se acerca a P, el tiempo que tarda en recorrer la distancia disminuye.
b) Grafica posición-tiempo para la “partícula”. A medida que los intervalos de tiempo se vuelven más y más pequeños, la velocidad promedio para ese intervalo, igual a la pendiente de la línea punteada que conecta P y la Q apropiada, se aproxima a la línea tangente en P. La velocidad instantánea en P es la pendiente de la línea tangente en el tiempo t1
Considérese el movimiento en línea recta de una partícula entre los puntos P y Q sobre el eje x, como se ve en la figura 2.7a. A medida que Q se va acercando más y más a P, el tiempo necesario para recorrer la distancia se vuelve progresivamente más pequeño. La velocidad promedio para cada intervalo de tiempo es la pendiente de la línea punteada correspondiente en la gráfica espacio-tiempo mostrada en la figura 2.7b Conforme Q se acerca a P, el intervalo de tiempo se aproxima a cero y la pendiente de la línea punteada se acerca a la de la línea tangente azul a la curva en P. La pendiente de esta línea se define como la velocidad instantánea en el tiempo ti, en otras palabras,
En la notación del cálculo, este límite se conoce como la derivada de X respecto de t, y se escribe dx/dk
De aquí en adelante se empleará la palabra velocidad para designara la velocidad instantánea. Cuando interese la velocidad promedio, se empleará siempre el adjetivo promedio.
La rapidez de una partícula se defines como la magnitud de su velocidad. La rapidez no tiene dirección asociada y, en consecuencia, no lleva signo algebraico. Por ejemplo, si una partícula tiene una velocidad de +25 m/s y otra partícula tiene la velocidad de –25m/s, las dos tiene una rapidez de 25m/s. El velocímetro de un automóvil indica la rapidez, no la velocidad.
También es posible utilizar una técnica matemática conocida como integración para determinar el desplazamiento de una partícula si se conoce su velocidad como una función del tiempo. Debido a que quizá los procedimientos de integración no sean familiares para muchos estudiantes, el tema se trata (opcionalmente).
EJEMPLO El proceso de límite
La posición de una partícula que se mueve a lo largo del eje x varía en el tiempo de acuerdo con la expresión x = (3 m/s2) t2, donde x está en metros y t en segundos. Encuentre la velocidad en cualquier tiempo.
Fig. 2.9 Grafica posición-tiempo para una partícula que tienen una coordenada x que varia en el tiempo según x=3t2. Observe que la velocidad instantánea en t=3s es igual ala pendiente de la línea delgada tangente a la curva en ese instante.
Razonamiento y solución La gráfica posición-tiempo para este movimiento se muestra en la figura 2.9 se puede calcular la velocidad en cualquier tiempo utilizando la definición de la velocidad instantánea (ecuación 2.3.5). Si la coordenada inicial de la partícula al tiempo t es
xi = 3t2, entonces la coordenada a un tiempo posterior ∆t + t es:
Para encontrar la velocidad instantánea, se toma el límite de esta expresión conforme ∆t se acerca a cero, como muestra la ecuación 2.9. Al hacerlo así, vemos que el término 3 ∆t se va a cero, por lo que:
Advierta que esta expresión brinda la velocidad en cualquier tiempo t. Nos indica que v crece linealmente en el tiempo. Por ello se encuentra directamente la velocidad en algún tiempo específico de la expresión v = (6 m/s2) t. Por ejemplo, si t = 3.0 s, la velocidad es v= (6 m/s2) (30.5) = + 18 m/s. De nuevo, esto puede verificarse a partir de la pendiente de la gráfica (la línea verde) en t=3.0s.
El proceso límite también puede examinarse numéricamente. Por ejemplo, con las expresiones para ∆xy v se puede calcular el desplazamiento y la velocidad promedio para diversos intervalos de tiempo que inicien en t = 3.0 s. Los resultados de estos cálculos se presentan en la tabla 2.3.4.1 a medida que los intervalos de tiempo se vuelven más y más pequeños, la velocidad promedio se acerca al valor de la velocidad instantánea en t = 3.0 s, es decir, +18 m/s.
MOVIMIENTO UNIDIMENSIONAL CON ACELERACIÓN CONSTANTE
Si la aceleración de una partícula varía con el tiempo, el movimiento puede ser muy difícil de analizar. Sin embargo, un tipo muy común y simple de movimiento
unidimensional ocurre cuando la aceleración es constante o uniforme. Cuando la
aceleración es constante, la aceleración promedio es igual a la aceleración instantánea, en consecuencia, la velocidad aumenta o disminuye a la misma tasa durante todo el movimiento.
Si en la ecuación se reemplaza ā por a, se obtiene:
Por conveniencia se deja ti = 0 y tf sea. cualquier tiempo arbitrario t. Además, se deja que vi = v0 (, (la velocidad inicial en t = 0) y vf= v (la velocidad en cualquier tiempo arbitrario t). Con esta notación, se puede expresar la aceleración como:
Esta expresión permite determinar la velocidad en cualquier tiempo t si se conocen la velocidad inicial, la aceleración (constante) y el tiempo transcurrido.
Una gráfica velocidad-tiempo para este movimiento se muestra en la figura 2.10a. La gráfica es una línea recta cuya pendiente es la aceleración, a, lo que es consistente con el hecho de que a = dv/dt es una constante.
Advierta que si la aceleración fuera negativa, la pendiente de la figura 2.10a sería negativa. Si la aceleración es en la dirección opuesta a la velocidad, entonces la partícula se está desacelerando.
De acuerdo con esta gráfica y con la ecuación 2.4.1, vemos que la velocidad en cualquier tiempo t es la suma de la velocidad inicial, vo, y el cambio en la velocidad, at.
La gráfica de la aceleración contra el tiempo (Fig. 2.10 b) es una línea recta con
una pendiente de cero, ya que la aceleración es constante.
Fig. 2.10 Una partícula que se mueve a lo largo del eje x con aceleración constante a;
a) gráfica velocidad-tiempo,
b) gráfica aceleración-tiempo
c) gráfica posición-tiempo.
Puesto que la velocidad varía linealmente en el tiempo, según la ecuación 1.8, es posible expresar la velocidad promedio en cualquier intervalo de tiempo como la media aritmética de la velocidad inicial, vo, y de la velocidad final, v:
IMPERBINCULOS DE INTERÉS.
Movimiento PARABOLICO.
http://www.sc.ehu.es/sbweb/fisica/cinematica/parabolico/maximo/maximo.htm
El siguiente link tiene información necesaria para el Movimiento Rectilíneo.
Pagina de Movimiento Rectilineo
Este link te enviara a un foro sobre la matemática y la Física llamado el Tío Petros.
Tio Petros
Este te redirecciona a una paginacon todo sobre la Matemática y su Importancia.
La Matemática y su Importancia
Vídeos de Calculo para mejorar el aprendizaje de la Física.
VIDEOS
El siguiente link tiene información necesaria para el Movimiento Rectilíneo.
Pagina de Movimiento Rectilineo
Este link te enviara a un foro sobre la matemática y la Física llamado el Tío Petros.
Tio Petros
Este te redirecciona a una paginacon todo sobre la Matemática y su Importancia.
La Matemática y su Importancia
Vídeos de Calculo para mejorar el aprendizaje de la Física.
VIDEOS






























